Calcular Volumen de un Prisma Rectangular

Calculadora de volumen de un prisma rectangular

Descripción, cuantas caras, aristas y vertices tiene un prisma rectangular

El prisma rectangular, también conocido como prisma cuadrangular, ortoedro, cuboide o paralelepípedo rectangular, es una figura que si se le hace un corte transversal en cualquier parte de su largo siempre mantiene la figura de un rectángulo.

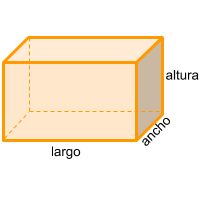
Tiene 6 caras, las caras que se intersectan forman ángulos de 90 grados y las caras opuestas son paralelas, tiene 12 aristas y 8 vértices.

Cuando tenemos 2 de las 3 longitudes (alto, ancho, largo) son iguales entonces estamos presentes a un prisma cuadrado y si las 3 longitudes (alto, ancho, largo) son iguales entonces estamos presentes a un cubo o hexaedro; aún así tanto el prisma cuadrado como el cubo son prismas rectangulares.

En que se parece un prisma rectangular

Podemos encontrar muchos objetos en forma de prisma rectangular. El prisma rectangular se parece a una pieza de lego, una caja de leche o jugo, un ladrillo, una caja de zapatos, una pecera, un contenedor, e incluso a un ¡edificio!, ¿puedes pensar en alguno más? déjanos un comentario en la caja de comentarios al final de la página.

Fórmula del volumen de un prisma rectangular

Para calcular el volumen de un prisma rectangular se calcula de la misma forma que todos los prismas, donde se toma el área de la base y se multiplica por su largo. En este caso la base del prisma rectangular es un rectángulo por lo tanto se calcula el área del rectángulo que lo forma. Es decir que finalmente se multiplica el alto del rectángulo, el ancho del rectángulo y luego el largo del prisma. También puedes utilizar la calculadora online para calcular el volumen del prisma rectangular automáticamente.

Volumen de otras figuras

Calcular volumen de distintas figuras geométricas: