Calcular Volumen de un Prisma Hexagonal
Calculadora de volumen de un prisma hexagonal
Descripción, cuantas caras, aristas y vertices tiene un prisma hexagonal
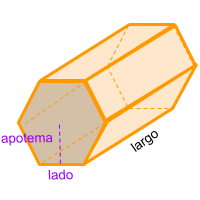
El prisma hexagonal, es una figura formada por 8 caras, 2 de las cuales son hexágonos iguales y paralelos y forman las bases en los extremos de la figura y otras 6 caras que son paralelogramos. Además cuenta con 18 aristas y 12 vértices. Si se le hace un corte transversal en cualquier parte de su largo siempre mantiene la figura de un hexágono.
Fórmula del volumen de un prisma hexagonal
Para calcular el volumen de un prisma hexagonal se calcula de la misma forma que todos los prismas, donde se toma el área de la base y se multiplica por su largo. En este caso, la base del prisma hexagonal es un hexágono, por lo tanto, se calcula el área del hexágono que lo forma.
Entonces para calcular el área del hexágono (área base), multiplicamos el perímetro del hexágono por su apotema y dividimos en dos. Luego esta área base que logramos calcular, la multiplicamos por el largo y obtenemos el volumen del prisma hexagonal.
Recodemos que la apotema, es la distancia del centro del polígono hasta el medio de uno de sus lados. Y recordemos también que el perímetro de un hexágono es la suma de todos sus lados o que es lo mismo un lado multiplicado por 6. También puedes utilizar la calculadora online para calcular el volumen del prisma hexagonal automáticamente.
Explicación de fórmula y fórmula alternativa:
La fórmula para calcular el volumen de un prisma es siempre la misma:
Volumen prisma = Área base × Largo
En este caso, el área de la base del prisma es el área de un hexágono por lo que tenemos que:
Para calcular el perímetro tenemos que:
Perímetro = 6 × Lado
Por lo tanto reemplazando el perímetro con los datos de arriba finalmente obtendremos la fórmula principal presentada.
También existe otra fórmula que no requiere de la apotema. Esto se da ya que la apotema también se puede calcular a partir de un lado:
Por lo tanto, otra forma de expresar la fórmula del volumen del prisma hexagonal sin conocer la apotema es:
Volumen de otras figuras
Calcular volumen de distintas figuras geométricas:
